Algoritmo de Dijkstra

También llamado algoritmo de caminos mínimos, es un algoritmo para la determinación del camino más corto dado un vértice origen al resto de vértices en un grafo con pesos en cada arista. Su nombre se refiere a Edsger Dijkstra, quien lo describió por primera vez en 1959.
      
     La idea subyacente en este algoritmo consiste en ir explorando todos los caminos más cortos que parten del vértice origen y que llevan a todos los demás vértices; cuando se obtiene el camino más corto desde el vértice origen, al resto de vértices que componen el grafo, el algoritmo se detiene.
   
    El algoritmo es una especialización de la búsqueda de costo uniforme, y como tal, no funciona en grafos con aristas de costo negativo (al elegir siempre el nodo con distancia menor, pueden quedar excluidos de la búsqueda nodos que en próximas iteraciones bajarían el costo general del camino al pasar por una arista con costo negativo).

Ejemplo

El siguiente ejemplo se desarrollará con el fin de encontrar el camino más corto desde a hasta z:

Dijkstrapaso0.jpg

Leyenda:

• Rojo: Aristas y vértices pertenecientes a la solución momentánea.
• Azul: Aristas y vértices candidatos.

Paso 1

Dijkstrapaso1.jpg

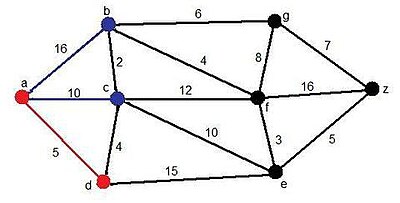
En este primer paso, podemos apreciar que hay tres candidatos: Los vértices b, c y d. En este caso, hacemos el camino desde el vértice a, hasta el vértice d, ya que es el camino más corto de los tres.
Solución momentánea:

• Camino: AD
• Distancia:5

Paso 2

Dijkstrapaso2.jpg

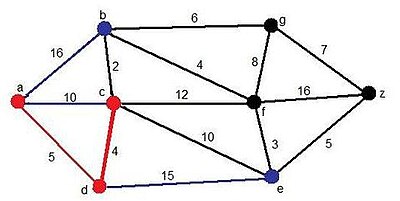
Ahora, vemos que se añade un nuevo candidato, el vértice e, y el vértice c, pero esta vez a través del d. Pero el camino mínimo surge al añadir el vértice c.
Solución momentánea:

• Camino: ADC
• Distancia:9

Paso 3

Dijkstrapaso4.jpg

En este paso no se añade ningún candidato más puesto que el último vértice es el mismo que en el paso anterior. En este caso el camino mínimo hallado es el siguiente:
Solución momentánea:

• Camino: ADCB
• Distancia:11

Paso 4

Dijkstrapaso5.jpg

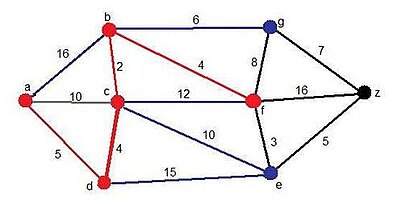
Como podemos comprobar, se han añadido dos candidatos nuevos, los vértices f y g, ambos a través del vértice b. El mínimo camino hallado en todo el grafo hasta ahora es el siguiente:
Solución momentánea:

• Camino: ADCBF
• Distancia:15

Paso 5

Dijkstrapaso6.jpg

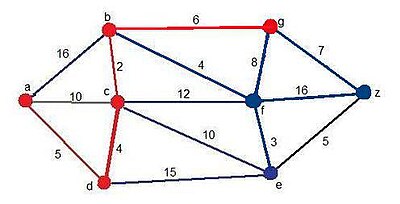
En este antepenúltimo paso, se añaden tres vértices candidatos, los vértices g, z y e. Este último ya estaba pero en esta ocasión aparece a través del vértice f. En este caso el camino mínimo, que cambia un poco con respecto al enterior, es:
Solución momentánea:

• Camino: ADCBF
• Distancia:17

Paso 6

Dijkstrapaso7.jpg

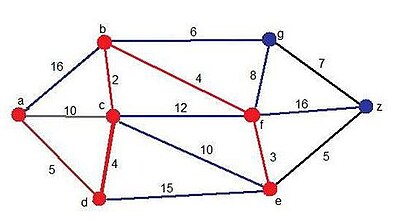
En el penúltimo paso, vuelve a aparecer otro candidato: el vértice z, pero esta vez a través del vértice g. De todas formas, el camino mínimo vuelve a cambiar para retomar el camino que venía siguiendo en los pasos anteriores:
Solución momentáneeea:

• Camino: ADCBFE
• Distancia:18

Paso 7

Dijkstrapaso8.jpg

Por fin, llegamos al último paso, en el que sólo se añade un candidato, el vértice z a través del e. El camino mínimo y final obtenido es:
Solución Final:

• Camino: ADCBFEZ
• Distancia:23.

Pseudo-codigo:

**función Dijkstra** (Grafo G, nodo_salida s)
  //Usaremos un vector para guardar las distancias del nodo salida al resto
  entero distancia[n] //Inicializamos el vector con distancias iniciales
  booleano visto[n] //vector de boleanos para controlar los vertices de los que ya tenemos la distancia mínima
  **para cada** w ∈ V[G] **hacer**
     **Si** (no existe arista entre s y w) **entonces**
         distancia[w] = Infinito //puedes marcar la casilla con un -1 por ejemplo
     **Si_no**
         distancia[w] = peso (s, w)
     **fin si**
  **fin para**
  distancia[s] = 0
  visto[s] = cierto
  //n es el número de vertices que tiene el Grafo
  **mientras que** (no_esten_vistos_todos) **hacer**
     vertice = coger_el_minimo_del_vector distancia y que no este visto;
     visto[vertice] = cierto;
     **para cada** w ∈ sucesores (G, vertice) **hacer**
         **si** distancia[w]>distancia[vertice]+peso (vertice, w) **entonces**
            distancia[w] = distancia[vertice]+peso (vertice, w)
         **fin si**
     **fin para**
  **fin mientras**
**fin función**

Explicación:

Teniendo un grafo dirigido ponderado de N nodos no aislados, sea x el nodo inicial, un vector D de tamaño N guardará al final del algoritmo las distancias desde x al resto de los nodos.

1. Inicializar todas las distancias en D con un valor infinito relativo ya que son desconocidas al principio, exceptuando la de x que se debe colocar en 0 debido a que la distancia de x a x sería 0.
2. Sea a = x (tomamos a como nodo actual).
3. Recorremos todos los nodos adyacentes de a, excepto los nodos marcados, llamaremos a estos vi.
4. Si la distancia desde x hasta vi guardada en D es mayor que la distancia desde x hasta a sumada a la distancia desde a hasta vi; esta se sustituye con la segunda nombrada, esto es:
   si (Di > Da + d(a, vi)) entonces Di = Da + d(a, vi)
5. Marcamos como completo el nodo a.
6. Tomamos como próximo nodo actual el de menor valor en D (puede hacerse almacenando los valores en una cola de prioridad) y volvemos al paso 3 mientras existan nodos no marcados.

Una vez terminado al algoritmo, D estará completamente lleno.