Licenciatura en Sistemas - Blog Informativo - Grafos
miércoles, 21 de octubre de 2015
Grafos 1.3.5
Esta herramienta nos permite crear grafos de todo tipo y es de gran ayuda para el entendimiento de los grafos:
Algoritmo de Floyd Warshall
Definicion:
Sea G un grafo con m nodos, u 1 , u 2 , ..., u m suponga que queremos encontrar la matriz de caminos P para el grafo G. WARSHALL dio un algoritmo para este propósito que es mucho más eficiente que calcular las potencias de la matriz de adyacencia A y aplicar la proposición:

donde sea A la matriz de adyacencia y P = Pij la matriz de caminos de un grafo G entonces, Pij = 1 si y solo sí hay un numero positivo en la entrada ij de la matriz.
El algoritmo de Floyd-Warshall, descrito en 1959 por Bernard Roy, es un algoritmo de análisis sobre grafos para encontrar el camino mínimo en grafos dirigidos ponderados. El algoritmo encuentra el camino entre todos los pares de vértices en una única ejecución.
Pseudo-codigo:
Explicación:
Sea G un grafo con m nodos, u 1 , u 2 , ..., u m suponga que queremos encontrar la matriz de caminos P para el grafo G. WARSHALL dio un algoritmo para este propósito que es mucho más eficiente que calcular las potencias de la matriz de adyacencia A y aplicar la proposición:

donde sea A la matriz de adyacencia y P = Pij la matriz de caminos de un grafo G entonces, Pij = 1 si y solo sí hay un numero positivo en la entrada ij de la matriz.
El algoritmo de Floyd-Warshall, descrito en 1959 por Bernard Roy, es un algoritmo de análisis sobre grafos para encontrar el camino mínimo en grafos dirigidos ponderados. El algoritmo encuentra el camino entre todos los pares de vértices en una única ejecución.
Pseudo-codigo:
Floyd-Warshall (G)
n=|V [G]|
for (int i=1; i<=numeroNodos; i++)
for (int j=1; j<=numeroNodos; j++)
si Hay conexión MatrizdePeso[i][j]=peso;
else MatrizdePeso[i][j]=infinito;
MatrizNodoIntermedio[i][j]=j;
Si i=j
MatrizNodoIntermedio[i][j]=0;
MatrizdePeso[i][j]=0;
for(int k=1;k<=numeroNodos;k++)
for (int i=1;i<=numeroNodos;i++)
for (int j=1;j<=numeroNodos;j++)
a=MatrizdePeso[i][k]+MatrizdePeso[k][j];
if(a<MatrizdePeso[i][j])
{
MatrizdePeso[i][j]=a;
MatrizNodoIntermedio[i][j]=k;
}
return MatrizdePeso, MatrizNodoIntermedio;
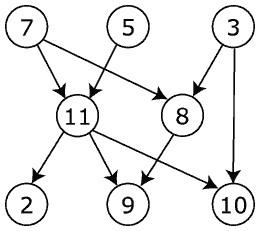
Dado un grafo G(V,A) se puede aplicar el algoritmo de Floyd para resolver el problema de encontrar el camino más corto de todos los vértices entre sí.
Inicio
Armar la matriz de adyacencia F, teniendo en cuenta que F(i,j)=0 si i = j (diagonal principal es 0). Además dónde no exista camino se debe indicar con infinito.
Para k desde 1 hasta n
Para i desde 1 hasta n
Para j desde 1 hasta n
F[i,j]=min(F[i,j], F[i,k] + F[k,j])
Fin para j
Fin para i
Fin para k
En la k-esima vuelta F[i, j] contendrá el valor del camino más corto que una al vértice i con el j tal que dicho camino no pase por un vértice con número mayor que k.
La matriz resultante es la de los mínimos caminos entre cada nodo. Si se quiere saber cual es dicho camino, se debe armar un árbol a medida tomando como numero de nodo a k cada vez que se detecta que hubo una optimización.
Debido a su triple ciclo anidado es obviamente O(N^3).
Inicio
Armar la matriz de adyacencia F, teniendo en cuenta que F(i,j)=0 si i = j (diagonal principal es 0). Además dónde no exista camino se debe indicar con infinito.
Para k desde 1 hasta n
Para i desde 1 hasta n
Para j desde 1 hasta n
F[i,j]=min(F[i,j], F[i,k] + F[k,j])
Fin para j
Fin para i
Fin para k
En la k-esima vuelta F[i, j] contendrá el valor del camino más corto que una al vértice i con el j tal que dicho camino no pase por un vértice con número mayor que k.
La matriz resultante es la de los mínimos caminos entre cada nodo. Si se quiere saber cual es dicho camino, se debe armar un árbol a medida tomando como numero de nodo a k cada vez que se detecta que hubo una optimización.
Debido a su triple ciclo anidado es obviamente O(N^3).
Pronto se estará publicando la implementacion en pascal.
Algoritmo de Dijkstra
También llamado algoritmo de caminos mínimos, es un algoritmo para la determinación del camino más corto dado un vértice origen al resto de vértices en un grafo con pesos en cada arista. Su nombre se refiere a Edsger Dijkstra, quien lo describió por primera vez en 1959.
La idea subyacente en este algoritmo consiste en ir explorando todos los caminos más cortos que parten del vértice origen y que llevan a todos los demás vértices; cuando se obtiene el camino más corto desde el vértice origen, al resto de vértices que componen el grafo, el algoritmo se detiene.
El algoritmo es una especialización de la búsqueda de costo uniforme, y como tal, no funciona en grafos con aristas de costo negativo (al elegir siempre el nodo con distancia menor, pueden quedar excluidos de la búsqueda nodos que en próximas iteraciones bajarían el costo general del camino al pasar por una arista con costo negativo).
El siguiente ejemplo se desarrollará con el fin de encontrar el camino más corto desde a hasta z:
Leyenda:
Paso 1
En este primer paso, podemos apreciar que hay tres candidatos: Los vértices b, c y d. En este caso, hacemos el camino desde el vértice a, hasta el vértice d, ya que es el camino más corto de los tres.
Solución momentánea:
Paso 2
Ahora, vemos que se añade un nuevo candidato, el vértice e, y el vértice c, pero esta vez a través del d. Pero el camino mínimo surge al añadir el vértice c.
Solución momentánea:
Paso 3
En este paso no se añade ningún candidato más puesto que el último vértice es el mismo que en el paso anterior. En este caso el camino mínimo hallado es el siguiente:
Solución momentánea:
Paso 4
Como podemos comprobar, se han añadido dos candidatos nuevos, los vértices f y g, ambos a través del vértice b. El mínimo camino hallado en todo el grafo hasta ahora es el siguiente:
Solución momentánea:
Paso 5
En este antepenúltimo paso, se añaden tres vértices candidatos, los vértices g, z y e. Este último ya estaba pero en esta ocasión aparece a través del vértice f. En este caso el camino mínimo, que cambia un poco con respecto al enterior, es:
Solución momentánea:
Paso 6
En el penúltimo paso, vuelve a aparecer otro candidato: el vértice z, pero esta vez a través del vértice g. De todas formas, el camino mínimo vuelve a cambiar para retomar el camino que venía siguiendo en los pasos anteriores:
Solución momentáneeea:
Paso 7
Por fin, llegamos al último paso, en el que sólo se añade un candidato, el vértice z a través del e. El camino mínimo y final obtenido es:
Solución Final:
La idea subyacente en este algoritmo consiste en ir explorando todos los caminos más cortos que parten del vértice origen y que llevan a todos los demás vértices; cuando se obtiene el camino más corto desde el vértice origen, al resto de vértices que componen el grafo, el algoritmo se detiene.
El algoritmo es una especialización de la búsqueda de costo uniforme, y como tal, no funciona en grafos con aristas de costo negativo (al elegir siempre el nodo con distancia menor, pueden quedar excluidos de la búsqueda nodos que en próximas iteraciones bajarían el costo general del camino al pasar por una arista con costo negativo).
Ejemplo
El siguiente ejemplo se desarrollará con el fin de encontrar el camino más corto desde a hasta z:
 |
| Dijkstrapaso0.jpg |
Leyenda:
- Rojo: Aristas y vértices pertenecientes a la solución momentánea.
- Azul: Aristas y vértices candidatos.
Paso 1
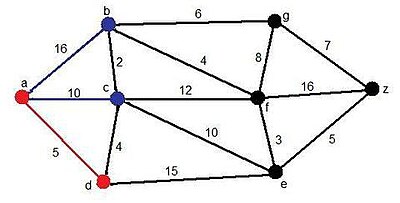 |
| Dijkstrapaso1.jpg |
En este primer paso, podemos apreciar que hay tres candidatos: Los vértices b, c y d. En este caso, hacemos el camino desde el vértice a, hasta el vértice d, ya que es el camino más corto de los tres.
Solución momentánea:
- Camino: AD
- Distancia:5
Paso 2
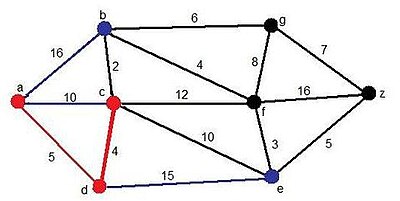 |
| Dijkstrapaso2.jpg |
Ahora, vemos que se añade un nuevo candidato, el vértice e, y el vértice c, pero esta vez a través del d. Pero el camino mínimo surge al añadir el vértice c.
Solución momentánea:
- Camino: ADC
- Distancia:9
Paso 3
 |
| Dijkstrapaso4.jpg |
En este paso no se añade ningún candidato más puesto que el último vértice es el mismo que en el paso anterior. En este caso el camino mínimo hallado es el siguiente:
Solución momentánea:
- Camino: ADCB
- Distancia:11
Paso 4
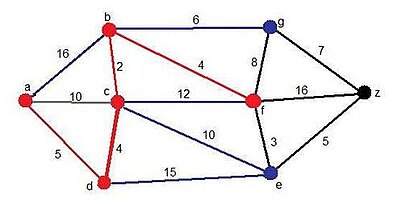 |
| Dijkstrapaso5.jpg |
Como podemos comprobar, se han añadido dos candidatos nuevos, los vértices f y g, ambos a través del vértice b. El mínimo camino hallado en todo el grafo hasta ahora es el siguiente:
Solución momentánea:
- Camino: ADCBF
- Distancia:15
Paso 5
 |
| Dijkstrapaso6.jpg |
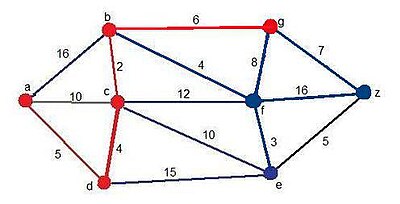
En este antepenúltimo paso, se añaden tres vértices candidatos, los vértices g, z y e. Este último ya estaba pero en esta ocasión aparece a través del vértice f. En este caso el camino mínimo, que cambia un poco con respecto al enterior, es:
Solución momentánea:
- Camino: ADCBF
- Distancia:17
Paso 6
 |
| Dijkstrapaso7.jpg |
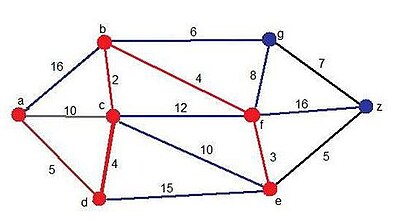
En el penúltimo paso, vuelve a aparecer otro candidato: el vértice z, pero esta vez a través del vértice g. De todas formas, el camino mínimo vuelve a cambiar para retomar el camino que venía siguiendo en los pasos anteriores:
Solución momentáneeea:
- Camino: ADCBFE
- Distancia:18
Paso 7
 |
| Dijkstrapaso8.jpg |
Por fin, llegamos al último paso, en el que sólo se añade un candidato, el vértice z a través del e. El camino mínimo y final obtenido es:
Solución Final:
- Camino: ADCBFEZ
- Distancia:23.
Pseudo-codigo:
**función Dijkstra** (Grafo G, nodo_salida s)
//Usaremos un vector para guardar las distancias del nodo salida al resto
entero distancia[n] //Inicializamos el vector con distancias iniciales
booleano visto[n] //vector de boleanos para controlar los vertices de los que ya tenemos la distancia mínima
**para cada** w ∈ V[G] **hacer**
**Si** (no existe arista entre s y w) **entonces**
distancia[w] = Infinito //puedes marcar la casilla con un -1 por ejemplo
**Si_no**
distancia[w] = peso (s, w)
**fin si**
**fin para**
distancia[s] = 0
visto[s] = cierto
//n es el número de vertices que tiene el Grafo
**mientras que** (no_esten_vistos_todos) **hacer**
vertice = coger_el_minimo_del_vector distancia y que no este visto;
visto[vertice] = cierto;
**para cada** w ∈ sucesores (G, vertice) **hacer**
**si** distancia[w]>distancia[vertice]+peso (vertice, w) **entonces**
distancia[w] = distancia[vertice]+peso (vertice, w)
**fin si**
**fin para**
**fin mientras**
**fin función**
Explicación:
Teniendo un grafo dirigido ponderado de N nodos no aislados, sea x el nodo inicial, un vector D de tamaño N guardará al final del algoritmo las distancias desde x al resto de los nodos.- Inicializar todas las distancias en D con un valor infinito relativo ya que son desconocidas al principio, exceptuando la de x que se debe colocar en 0 debido a que la distancia de x a x sería 0.
- Sea a = x (tomamos a como nodo actual).
- Recorremos todos los nodos adyacentes de a, excepto los nodos marcados, llamaremos a estos vi.
- Si la distancia desde x hasta vi guardada en D es mayor que la distancia desde x hasta a sumada a la distancia desde a hasta vi; esta se sustituye con la segunda nombrada, esto es:
si (Di > Da + d(a, vi)) entonces Di = Da + d(a, vi) - Marcamos como completo el nodo a.
- Tomamos como próximo nodo actual el de menor valor en D (puede hacerse almacenando los valores en una cola de prioridad) y volvemos al paso 3 mientras existan nodos no marcados.
martes, 20 de octubre de 2015
TEORÍA DE GRAFOS: Teorema de los cuatro colores.
En 1852 Francis Guthrie planteó el problema de
los cuatro colores.
Otro problema famoso relativo a los grafos: ¿Cuántos colores son
necesarios para dibujar un mapa político, con la condición obvia que
dos países adyacentes no puedan tener el mismo color?
Se supone que los países son de un solo pedazo, y que el mundo es esférico o plano. En un mundo en forma de toroide; el teorema siguiente no es válido: Cuatro colores son siempre suficientes para colorear un mapa.
El mapa siguiente muestra que tres colores no bastan: Si se empieza por el país central a y se esfuerza uno en utilizar el menor número de colores, entonces en la corona alrededor de a alternan dos colores. Llegando al país h se tiene que introducir un cuarto color. Lo mismo sucede en i si se emplea el mismo método.
La forma precisa de cada país no importa; lo único relevante es saber qué país toca a qué otro. Estos datos están incluidos en el grafo donde los vértices son los países y las aristas conectan los que justamente son adyacentes. Entonces la cuestión equivale a atribuir a cada vértice un color distinto del de sus vecinos.
Hemos visto que tres colores no son suficientes, y demostrar que con cinco siempre se llega, es bastante fácil. Pero el teorema de los cuatro colores no es nada obvio. Prueba de ello es que se han tenido que emplear ordenadores para acabar la demostración (se ha hecho un programa que permitió verificar una multitud de casos, lo que ahorró muchísimo tiempo a los matemáticos). Fue la primera vez que la comunidad matemática aceptó una demostración asistida por ordenador, lo que ha creado una fuerte polémica dentro de la comunidad matemática, llegando en algunos casos a plantearse la cuestión de que esta demostración y su aceptación es uno de los momentos que han generado una de las más terribles crisis en el mundo matemático.
 |
| En 1852 Francis Guthrie planteó el problema de los cuatro colores. |
Se supone que los países son de un solo pedazo, y que el mundo es esférico o plano. En un mundo en forma de toroide; el teorema siguiente no es válido: Cuatro colores son siempre suficientes para colorear un mapa.
El mapa siguiente muestra que tres colores no bastan: Si se empieza por el país central a y se esfuerza uno en utilizar el menor número de colores, entonces en la corona alrededor de a alternan dos colores. Llegando al país h se tiene que introducir un cuarto color. Lo mismo sucede en i si se emplea el mismo método.
La forma precisa de cada país no importa; lo único relevante es saber qué país toca a qué otro. Estos datos están incluidos en el grafo donde los vértices son los países y las aristas conectan los que justamente son adyacentes. Entonces la cuestión equivale a atribuir a cada vértice un color distinto del de sus vecinos.
Hemos visto que tres colores no son suficientes, y demostrar que con cinco siempre se llega, es bastante fácil. Pero el teorema de los cuatro colores no es nada obvio. Prueba de ello es que se han tenido que emplear ordenadores para acabar la demostración (se ha hecho un programa que permitió verificar una multitud de casos, lo que ahorró muchísimo tiempo a los matemáticos). Fue la primera vez que la comunidad matemática aceptó una demostración asistida por ordenador, lo que ha creado una fuerte polémica dentro de la comunidad matemática, llegando en algunos casos a plantearse la cuestión de que esta demostración y su aceptación es uno de los momentos que han generado una de las más terribles crisis en el mundo matemático.
TEORÍA DE GRAFOS: Para empezar... ¿Qué son los grafos?
HISTORIA
El nacimiento del concepto GRAFOS se puede situar, por el año 1730, cuando Euler (matemático) se convirtió en el padre de la Teoría de Grafos al modelar un famoso problema no resuelto, llamado el "problema de los puentes de Königsberg".
Un río con dos islas atraviesa la ciudad. Las islas estan unidas, entre si y con las orillas, a través de siete puentes. El problema consistía en establecer un recorrido que pasara una y solo una vez por cada uno de los siete puentes, partiendo de cualquier punto y regresando al mismo lugar.
Para probar que no era posible, Euler sustituyó cada zona de partida por un punto y cada puente por un arco, creando así un grafo, el primer grafo, diseñado para resolver un problema.
DEFINICION
Un grafo en el ámbito de las ciencias de la computación es una estructura de datos, en concreto un tipo abstracto de datos (TAD), que consiste en un conjunto de nodos (también llamados vértices) y un conjunto de arcos (aristas) que establecen relaciones entre los nodos. El concepto de grafo TAD desciende directamente del concepto matemático de grafo.
Un nodo es la unidad sobre la que se construye el grafo y puede tener cero o más nodos hijos conectados a él.
Las aristas son las líneas con las que se unen los vértices o nodos de un grafo y con la que se construyen también caminos.
Informalmente se define como G = (V, E), siendo los elementos de V los vértices, y los elementos de E, las aristas (edges en inglés). Formalmente, un grafo, G, se define como un par ordenado, G = (V, E), donde V es un conjunto finito y E es un conjunto que consta de dos elementos de V.
Muchas redes de uso cotidiano pueden ser modeladas con un grafo: una red de carreteras que conecta ciudades, una red eléctrica o los mapas de las líneas del ferrocarril.
Estructura de lista
- Lista de incidencia - Las aristas son representadas con un vector de pares (ordenados, si el grafo es dirigido), donde cada par representa una de las aristas.
- Lista de adyacencia - Cada vértice tiene una lista de vértices los cuales son adyacentes a él. Esto causa redundancia en un grafo no dirigido (ya que A existe en la lista de adyacencia de B y viceversa), pero las búsquedas son más rápidas, al costo de almacenamiento extra.
En esta estructura de datos la idea es asociar a cada vértice i del grafo una lista que contenga todos aquellos vértices j que sean adyacentes a él. De esta forma sólo reservará memoria para los arcos adyacentes a "i" y no para todos los posibles arcos que pudieran tener como origen "i". El grafo, por tanto, se representa por medio de un vector de n componentes (si |V|=n) donde cada componente va a ser una lista de adyacencia correspondiente a cada uno de los vértices del grafo. Cada elemento de la lista consta de un campo indicando el vértice adyacente. En caso de que el grafo sea etiquetado, habrá que añadir un segundo campo para mostrar el valor de la etiqueta.
Estructuras matriciales:
- Matriz de incidencia - El grafo está representado por una matriz de A (aristas) por V (vértices), donde [arista, vértice] contiene la información de la arista (1 - conectado, 0 - no conectado)
- Matriz de adyacencia - El grafo está representado por una matriz cuadrada M de tamaño n2, donde n es el número de vértices. Si hay una arista entre un vértice x, y un vértice y, entonces el elemento m[x,y] es 1, de lo contrario, es 0.
Suscribirse a:
Comentarios (Atom)